Matthew Williams
"Please tell me inner tube water polo is a real thing and that it's as hilarious to watch as it sounds."
"Oh it's definitely real and exactly as ridiculous and glorious as it sounds."
Those were the first words I ever shared with my partner Mattea when we matched on Bumble almost two years ago. I brought her to a game on our fifth date, and she's been cheering us on ever since. As silly as it sounds, inner tube water polo has been a huge part of my life and, along with Mattea, helped me through the last year of my PhD. Writing my dissertation in the office was miserable most days, but being able to take breaks to strategize the next game with other grads kept me going.
If you've never seen a game before, it plays out like water polo, except all the players sit in inner tubes, and that one change makes the game so much more accessible and absurd. For graduate students in the math department at Colorado State University, inner tube water polo has been a staple for more than a decade, spanning 21 teams and 67 players, including students, alumni, partners, and friends of the department.
Read the full article.
New Knot News!
James Fantin-Hardesty
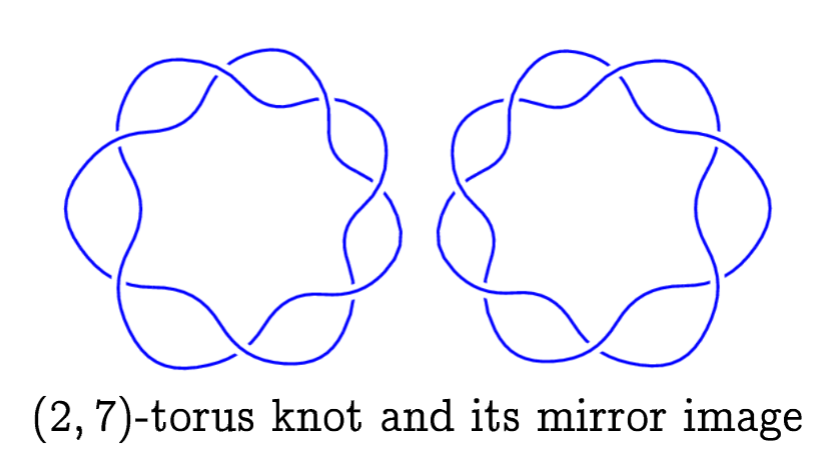
A decades old knot theory conjecture has been unraveled. The conjecture asks, is the unknotting number (the number of crossing changes (or "cuts") needed to transform a knot into a simple loop) additive under addition? Or more specifically, is the unknotting number of the connected sum of two knots simply the sum of their individual unknotting numbers? It turns out, the answer is a surprising no. This means that by combining two knots together, you can end up with a knot that is simpler to unravel.
Mathematicians Mark Brittenham and Susan Hermiller disproved the conjecture with a simple counter example. They showed that by constructing the connected sum of the $(2,7)$-torus knot and its mirror image, the resulting knot has an unknotting number of 5, meaning it would take 5 crossing changes to turn the knot into the unknot. Whereas the two knots each have an unknotting number of 3. And as we all know, 5 does not equal 6.
Principia Musica?
Eamon Gannon
The music theorist is a close cousin of the mathematician, sharing a predisposition for pedantry and abstruse nonsense.
...
In Defense of Paper
Fernando Herrera Valverde
With the creation of tablets and other personal computing devices, the last two decades have changed the way we work in most fields, mathematics is no exception. Where mathematicians once hunched over notebooks, they now tap on tablets. The transition feels inevitable—why wouldn't we want searchable notes, infinite paper, and the ability to reorganize our thoughts with a swipe?
...


